Rajasthan Board RBSE Class 12 Maths Chapter 15 Linear Programming Ex 15.1
Solve the following linear programming problem by graphical method :
Question 1.
Minimize Z = -3x + Ay
subject to the constraints x + 2y ≤ 8
3x + 2y ≤ 12
and x ≥ 0, y ≥ 0
Solution:
Converting the given inequations into equations
x + 2y = 8
3x + 2y = 12
Region represented by x + 2y ≤ 8 : The line x + 2y = 8 meets the coordinate axis at A(8, 0) and B(0, 4).
x + 2y = 8
| X | 8 | 0 |
| y | 0 | 4 |
A(8,0),B(0,10)
Join the points A and B to obtain the line. Clearly (0, 0) satisfies the inequation x + 2y = 8. So the region containing the origin represents the solution set of the inequation.
Region represented by 3x + 2y ≤ 12 : The line 3x + 2y = 12 meets the coordinate axis at C(4, 0) and D(0, 6).
3x + 2y = 12
| X | 4 | 0 |
| y | 0 | 6 |
C(4, 0); D(0,6)
Join the points C and D to obtain the line. Clearly (0, 0) satisfies the inequation 3x + 2y = 12. So the region containing. The origin represents the solution set of the inequations.
Region represented by x ≥ 0, y ≥ 0 : Since every point in the first quadrant satisfies these inequations. So the first quadrant is the region represented by the inequations x ≥ 0, y ≥ 0.
The shaded region OCEB represents the common region of the above inequations. This region is the feasible region of the given linear programming problem.

The coordinates of the comer points of the feasible region are O(0, 0), C(4, 0), E(2, 3) and 5(0, 4).
The point E(2, 3) has been obtained by solving the equations of the corresponding intersecting lines simultaneously.
The values of the objective function on these points are given in the following table :
| Point | x-coordinate | y-coordinate | Objective function Z = 3x + 4y |
| O | 0 | 0 | Z0 = -3(0) + 4(0) = 0 |
| C | 4 | 0 | Zc = -3(4) + 4(0) = -12 |
| E | 2 | 3 | ZE = -3(2) + 4(3) = 6 |
| B | 0 | 4 | ZB = -3(0) + 4(4) = 16 |
It is clear from the above table that the objective function has minimum value at comer point C(4, 0). So the minimum value of given linear programming problem at x = 4 and y = 0 is – 12.
Question 2.
Maximize Z = 3x + 4y
subject to the x + y ≤ 4
constraints x ≥ 0, y ≥ 0
Solution:
Converting the given inequations into equation x + y = 4
Region represented by x + y ≤ 4 : The line x + y = 4 meets the coordinate axis at A(4, 0) and B(0, 4).
| X | 4 | 0 |
| y | 0 | 4 |
A(4, 0); B(0,4)
Join the points A and B to obtain a line. Clearly (0, 0) satisfies the inequation x + 2y ≤ 4. So the region containing the origin represents the solution set of the inequation.
Region represented by x ≥ 0,y ≥ 0 : Since every point in the first quadrant satisfies these inequations. So the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0. The shaded region OAB represents the common region of the above inequations. This region is the feasible region of the given Linear Programming Problem.

The coordinates of the corner points of the shaded feasible region are O(0, 0), A(4.0) and B(0, 4).
The values of the objective function of these points are given in the following table :
| Point | x-coordinate | y-coordinate | Objective function Z = 3x + 4y |
| O | 0 | 0 | Z0 = 3(0) + 4(0) = 0 |
| A | 4 | 0 | ZA = 3(4) + 4(0) = 12 |
| B | 0 | 4 | ZB = 3(0) + 4(4) = 16 |
It is clear from the table, the objective function has maximum value at point B(0, 4).
So, the required solution of the given LPP, is x = 0, y = 4 and the maximum value is Z = 16.
Question 3.
Minimize Z = – 50x + 20y
Subject to the constraints
2x – y ≥- -5
3x + y ≥ 3
2x- 3y ≤ 12
and x ≥ 0, y ≥ 0
Solution:
Converting the given inequations into equations
2x – y = – 5 …..(1)
3x + y = 3 …..(2)
2x – 3y = 12 …..(3)
Region represented by 2x – y ≥ – 5 : The line 2x – y = -5 meets the coordinate axis at A(\(\frac { -5 }{ 2 } \),0) and B(0,5)
2x – y = -5
| X | -5/2 | 0 |
| y | 0 | 5 |
A(\(\frac { -5 }{ 2 } \),0) ;B (0,5)
Join the points A and B to obtain the line. Clearly (0, 0) satisfies the inequation 2x – y ≥ – 5. So the region containing the origin, represents the solution set of the inequation.
Region represented by 3x + y ≥ 3 : The line 3x + y = 3 meets the coordinate axis at A(1, 0) and B(0, 3).
3x + y = 3
| X | 1 | 0 |
| y | 0 | 3 |
C(1,0);D(0,3)
Join the points C to D to obtain the line. Clearly the point (0, 0) does not satisfy the inequation. So the region opposite to the origin represents the solution set of the inequation.
Region represented by 2x – 3y ≤ 12 : The line 2x – 3y = 12 meets the coordinate axis at E(6, 0) and F(0, -4).
2x – 3y = 12
| X | 6 | 0 |
| y | 0 | -4 |
E(6,0);F(0,-4)
Join the points E and F to obtain the line. Clearly (0, 0) satisfies the inequation 2x – 3y ≤ 12. So the region containing the origin represents the solution set of the inequation.
Region represented by x ≥ 0, y ≥ 0 : Since every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, y ≥ 0.
The point of intersection of lines 2x – y = -5 and 3x + y = 3 is G (\(\frac { -2 }{ 5 } \),\(\frac { 21 }{ 5 } \)).

The shaded area is an open and common region which satisfies the given constraints. This is the proper solution of the given LPP.
The value of the objective function on These points are given in following table:
| Point | x Coordenate | y Coordinal | z = -50x + 2y |
| B | 0 | 5 | zB = -50 x 0 + 20 x 5 = 100 |
| D | 0 | 3 | zD = -50 x 0+ 20 x 3 = 60 |
| C | 1 | 0 | zC = -50 x 1 + 20 x 0 = -50 |
| E | 6 | 0 | zE = -50 x 6 + 20 x 0 = -300 |
Clearly Z is minimum at x = 6 and y = 0
∵ Minimum value of Z = – 300
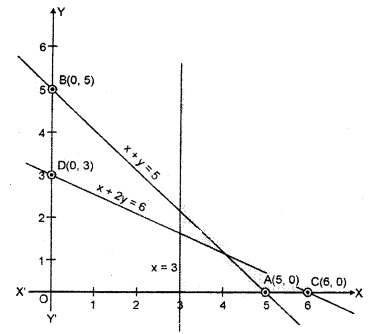
Question 4.
Minimize Z = 3x + 5y
Subject to the constraints
x + 3y ≥ 3
x + y ≥ 2
and x ≥ 0,y ≥ 0
Solution:
Converting the given inequations into equations
x + 3y = 3
x + y = 2
Region represented by x + 3y ≥ 3 : The line x + 3y = 3 meets the coordinate axis at A(3, 0) and B(0, 1).
x + 3y = 3
| X | 3 | 0 |
| y | 0 | l |
A(3, 0); B(0, 1)
Join the points A to 5 to obtain a line. Clearly (0,0) does not satisfy the inequation x + 3y ≥ 3. So the region opposite to the origin, represents the solution set of the inequation.
Region represented by x + y ≥ 2 : The line x + y = 2 meets the coordinate axis at points C(2, 0) and D(0, 2).
x + y = 2
| X | 2 | 0 |
| y | 0 | 2 |
C(2, 0); D(0, 2)
Join the points C to D to obtain the line. Clearly (0, 0) does not satisfy the inequation x + y ≥ 2.
So the region opposite to origin, represents the solution set of the inequation.
Region represented by x ≥ 0, y ≥ 0: Since every point in the first quadrant satisfies these inequations. So the first quadrant is the region represented by the equations x ≥ 0, y ≥ 0.
The point of intersection of lines x + 3y = 3 and x + y = 2 is E (\(\frac { 3 }{ 2 } \),\(\frac { 1 }{ 2 } \)).

The shaded region A ED is an open and common region of given inequations. This is the proper solution of the given linear programming problem.
The coordinates of the shaded region are A(3, 0), E (\(\frac { 3 }{ 2 } \),\(\frac { 1 }{ 2 } \)) and D(0, 2).
The values of the objective function of these points are given in following table :

Clearly Z is minimum at x = \(\frac { 3 }{ 2 } \) and y = \(\frac { 1 }{ 2 } \)
Therefore x = \(\frac { 3 }{ 2 } \) and y = \(\frac { 1 }{ 2 } \) is the required solution of the L.P. problem and the minimum value of Z is 7.
Question 5.
Evaluate maximum and minimum value, where Z = 3x + 9y
Subject to the constraints
x + 3y ≤ 60
x + y ≥ 10
x – y ≥ 0
and x ≥ 0, y ≥ 0
Solution:
Converting the given inequations into equations
x + 3y = 60 …..(1)
x + y = 10 …..(2)
x = 0, y = 0 ….(3)
Region represented by x + 3y ≤ 60: The line x + 3y = 60 meets the coordinate axis at A(60,0) and B(0, 20).
x + 3y = 60
| X | 60 | 0 |
| y | 0 | 20 |
A(60, 0); B(0, 20)
Join the points A to B to obtain the line.
Clearly (0,0) satisfies the inequation x + 3y ≤ 60. So the region containing the origin, represents the solution set of the inequation.
Region represented by x + y ≥ 10 : The line x + y = 10 meets the coordinate axis at point C(10,0) and D(0, 10).
x + y = 10
| X | 10 | 0 |
| y | 0 | 10 |
C(10, 0);D(0, 10)
Join point C to D to obtain the line.
Clearly (0, 0) does not satisfy the inequation x + y ≥ 10.
So the region opposite to origin, represents the solution set of the inequation.
Region represented by x – y ≥ 0 : The line x – y = 0 meets the coordinate axis at O(0, 0), E(5, 5).
| X | 0 | 5 |
| y | 0 | 5 |
O(0, 0); E(5, 5)
Join point O to E to obtain the line. Clearly (0, 0) satisfies the x – y ≥ 0. So the region cointaining origin represents the solution of inequation.
Region represented by x ≥ 0, y ≥ 0 : Since every point in the first quadrant satisfies these inequations. So the first qudrant is the region represented by the inequation x ≥ 0 and y ≥ 0.

The shaded region BDEF represents the solution region of the above inequations. This region is the feasible region of the given L.P.P.
The coordinates of the comer points of the shaded feasible region are (0, 10), (5, 5), (15, 15) and (0, 20). The point C(15, 15) is the point of intersection of lines x =y and x + 3y=60 and point E is the intersection point of lines x + y = 10 and x = y.
The values of the objective function on these points are given in the following table:
| Point | x-coordinate | y-coordinate | Objective function Z = 3x + 9y |
| D | 0 | 10 | ZP = 3(0) + 9(10) = 90 |
| E | 5 | 5 | ZE = 3(5) + 9(5) = 60 |
| F | 15 | 15 | ZF = 3(15) + 9(15) = 180 |
| B | 0 | 20 | ZH = 3(0) + 9(20) = 180 |
Clearly value of objective function Z is minimum at point E(5,5) where x = 5 and y = 5 and Z= 60 and the Z is maximum at two points C( 15, 15) and D(0, 20) where Z = 180.
Hence the Minimum value of Z = 60 and Maximum value of Z = 180.
Question 6.
Minimize Z = x + 2y
Subject to the constraints
2x + y ≥ 3
x + 2y ≥ 6
and x ≥ 0, y ≥ 0
Solution:
Converting the given inequations into equations
2x + y = 3 ….(1)
x + 2y = 6 ….(2)
Region represented by 2x + y ≥ 3 : The line 2x + y – 3 meets the coordinate axis at points A (\(\frac { 3 }{ 2 } \),0) and B(0. 3).
2x + y = 3
| X | 3/2 | 0 |
| y | 0 | 3 |
A(\(\frac { 3 }{ 2 } \),0);B(0,3)
Join the points ,A and B to get the line. Clearly (0,0) does not satisfy the inequation 2x + y ≥ 3. So the region opposite to the origin represents the solution set of the inequation.
Region represented by x + 2y ≥ 6 : The line x + 2y = 6 meets the coordinate axis at point C(6, 0) and D(0,3).
x + 2y = 6
| X | 6 | 0 |
| y | 0 | 3 |
C(6, 0); D(0, 3)
Join point C to D to obtain the line. Clearly (0,0) does not satisfy the inequation x + 2y ≥ 6. So the region opposite to the origin represents the solution set of the inequation.
Region represented by x ≥ 0 and y ≥ 0 : Since every point in the first quadrant satisfies the inequations. So the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.

In the shaded region on CB, each and every point on line CB is satisfying the given inequations.
So the values of the objective function on these points are given in the following table :
| Point | x-coordinate | v-coordinate | Objective function Z = x + 2y |
| 5 | 0 | 3 | ZB= 0 + 2(3) = 6 |
| C | 6 | 0 | Zc = 6 + 2(0) = 6 |
It is clear from the table that required solution of given L.P.P. every point is on line BC and the minimum value of Z = 6.
Question 7.
Find maximum and minimum value
where Z = 5x + 10y
Subject to the constraints
x + 2y ≤ 120
x + y ≥ 60
x – 2y ≥ 0
and x ≥ 0, y ≥ 0
Solution:
Converting the given inequations into equations
x + 2y = 120
x + y = 60
x – 2y = 0
Region represented by x + 2y ≤ 120 : The line x + 2y = 120 meets the coordinate axis at points ,4(120, 0) and B(0, 60).
x + 2y = 120
| X | 120 | 0 |
| y | 0 | 60 |
A(120,);B(0,60)
Join points A and B to obtain the line, clearly (0, 0) satisfies the given inequation. So the region containing the origin represents the solution set of the inequation x + 2y ≤ 120.
Region represented by x + y ≥ 60 : The line x + y = 60 meets the coordiante axis at point C(60,0) and B(0, 60).
x + y = 60
| X | 60 | 0 |
| y | 0 | 60 |
C(60,0) and D(0, 60).
Join the points C to 5 to obtain a line. Clearly (0,0) does not satisfy the given inequation x + y ≥ 60. So the region opposite to the origin represents the solution set of the inequation.
Region represented by x – 2y ≥ 0 : The line x = 2y meets the coordinate axis on origin (0,0) and any other points (60, 30).
x = 2y
| X | 0 | 60 |
| y | 0 | 30 |
O(0,0);E(60,30)
Join the points (0,0) and E(10,5) to obtain a line. Clearly (0, 0) satisfies the given inequation. So the region containing the origin represents the solution set of the inequation x – 2y ≥ 0.
Region represented by x ≥ 0, y ≥ 0 : Since every point in the first quadrant satisfies these inequation. So, the first quadrant is the region represented by the inequation x ≥ 0 and y ≥ 0.
The shaded region ACEF represents the common region of the above inequations. This region is the feasible region of the given LPP.
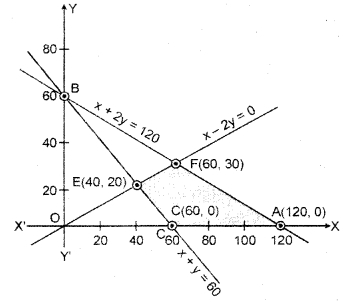
The point of intersection of lines x + 2y = 120 and x + y = 60 is (0, 60).
The point of intersection of lines x + 2y = 120 and x – 2y = 0 is (60,30) and the point of intersection of lines x + y = 60 and x – 2y = 0 is (20, 40).
The coordinates of the vertices (comer points) of the shaded feasible region are 4(120,0), C(60,0), £(40, 20) and F(60, 30).
The values of the objective function at these points are given in the following table.
| Point | x-coordinate | y-coordinate | Objective function Z = 5x + 10y |
| A | 120 | 0 | ZA = 5(120) + 10(0) = 600 |
| C | 60 | 0 | ZC = 5(60) + 10(0) = 300 |
| E | 40 | 20 | ZE = 5(40) + 10(20) = 400 |
| F | 60 | 30 | ZF = 5(60) + 10(30) = 600 |
Clearly the value of Z is minimum at C(60, 0) = 300 and the maximum value of Z= 600 at every point of line AF.
Question 8.
Maximize Z = x + y
Subject to the constraints
x – y ≤ -1
-x + y ≤ 0
and x ≤ 0,y ≤ 0
Solution:
Converting the given inequations into equations
x – y = – 1
-x + y = 0
Region represented by x – y ≤ -1 : Following are the points obtained by the line
x – y = -1
| X | -1 | 0 |
| y | 0 | 1 |
A(-1,0);B(0,1)
Join the points A and B to obtain the line. Clearly (0, 0) does not satisfy the inequation x – y ≤ -1. So the region opposite to the origin represent the solution set of the inequation.
Region represented by -x + y ≤ 0 : The line -x + y = 0 meets the coordinates axis at B(0,0) and C( 1,1).
-x + y = 0
| X | 0 | 1 |
| y | 0 | 1 |
O(0,0);C(1,1)
Join the points O and C to obtain this line.
Clearly (0,0) satisfies the inequation -x + y ≤ 0. So, the region containing the origin represents the solution set of this inequation.
Region represented by x ≥ 0, y ≥ 0 : Since every point in the quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.

It is clear from the figure that line joining point A(-1, 0) and B(0, 1) is parallel to the line joining point C(1,1) to D(2, 2). Hence there is no finite solution of the given LPP. Minimum and Maximum value do not exist.
Question 9.
Minimize
Z = 3x + 2y
Subject to the constraints
x + y ≥ 8
3x + 5y ≤ 15
and x ≥ 0,y ≥ 0
Solution:
Converting given inequations into equations
x + y = 8 ……(1)
3x + 5y = 15 …..(2)
Region represented by x + y ≥ 8 : The line x + y = 8, meets the coordinate axis at A(8, 0) and B(0, 8)
x + y = 8
| X | 8 | 0 |
| y | 0 | 8 |
A(8,0);B(0,8)
Join the points A and B to obtain the line.
Clearly, (0, 0) does not satisfy the inequation x + y ≥ 8. So the region opposite of the origin represents the solution set of the inequation x + y ≥ 8.
Region represented by 3x + 5y ≤ 15 : The line 3x + 5y = 15 meets the coordinate axis at A(5, 0) and B(0, 3).
3x + 5y = 15
| X | 5 | 1 |
| y | 0 | 3 |
A(5, 0);B(0, 3)
Join points A and B to obtain the line. Clearly (0,0) satisfies the inequation 3x + 5y ≤ 15. So, the region containing the origin represent the solution of the inequation 3x + 5y ≤ 15.
Region represented by x ≥ 0, y ≥ 0 : Since every point in the first quadrant satisfies the inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.

It is clear from the graph that there is no common feasible solution region. Therefore no value exists for given objective function.
Question 10.
Maximize Z = -x + 2y
Subject to the constraints
x ≥ 3
x + y ≥ 5
x + 2y ≥ 6
and x ≥ 0,y ≥ 0
Solution:
Converting the given inequations into equations
x = 3 …..(1)
x +y = 5 …..(2)
x + 2y = 6 …..(3)
y = 0 …..(4)
Region represented by x + y ≥ 5 : The line x + y = 5
meets the coordinate axis on points A(5,0) and B(0, 5).
x + y = 5
| X | 5 | 0 |
| y | 0 | 5 |
A(5,0);B(0,5)
Join the points A to 5 to obtain the line. Clearly (0, 0) does not satisfy the inequation 0 + 0 = 0 ≥ 5. So the opposite region to the origin represents the feasible solution region.
Region represented by x + 2y ≥ 6 : The line x + 2y = 6 meets the coordinate axis at point C(6,0) and D(0, 3).
x + 2y = 6
| X | 6 | 0 |
| y | 0 | 3 |
C(6,0);D(0,3)
Join point C to D to obtain the line. Clearly (0,0) does not satisfy the inequation 0 + 2(0) = 0 ≥ 6. So the region opposite to the origin represents the solution region of the inequation.
Region represented by x ≥ 3 and y ≥ 0 : Since every point in the first quadrant satisfies these inequations. So the first quadrant is the region represented by the inequations x ≥ 3 and y ≥ 0.
It is clear from the graph that there is no any common region of the given inequations.
Hence there does not exist any maximum value for the given inequations.
Leave a Reply