RBSE Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.1

RBSE Solutions for Class 9 Maths Chapter 4 Linear Equations in Two Variables Ex 4.1 is part of RBSE Solutions for Class 9 Maths. Here we have given Rajasthan Board RBSE Class 9 Maths Solutions Chapter 4 Linear Equations in Two Variables Exercise 4.1.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 9
Subject	Maths
Chapter	Chapter 4
Chapter Name	Linear Equations in Two Variables
Exercise	Ex 4.1
Number of Questions Solved	11
Category	RBSE Solutions

Rajasthan Board RBSE Class 9 Maths Solutions Chapter 4 Linear Equations in Two Variables Ex 4.1

Solve the following pair of equations graphically

Question 1.
x + 3y = 6; 2x – 3y = 12
Solution.
From the given (RBSESolutions.com) equations
x + 3y = 6 ⇒ x = 6 – 3y …(i)
when y = 1, x = 6 – 3 × 1 = 3
when y = 2, x = 6 – 3 × 2 = 0
when y = 0, x = 6 – 3 × 0 = 6
when y = – 1, x = 6 – 3 × – 1 = 9

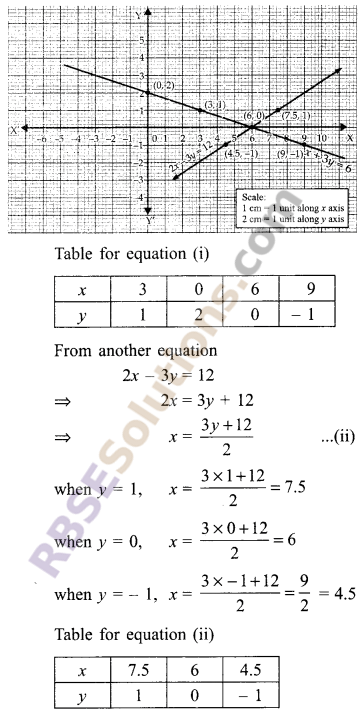
Now plotting and joining the points (RBSESolutions.com) from table 1 and table II on the same graph paper, we find their point of intersection is (6, 0).
Hence, (6, 0) is the solution of the pair of equations.

Question 2.
2x + y = 6; 2x – y + 2 = 0
Solution.
From the given equation
2x + y = 6 …(i)
Expressing y in terms of x, we get
y = 6 – 2x
when x = 0, y = 6 – 2 × 0 = 6

Now plotting and joining the (RBSESolutions.com) points from table I and II on the same graph paper, we find their point of intersection is (1, 4).
Hence, (1, 4) is the required solution.

Question 3.
x – 2y = 6; 3x – 6y = 0
Solution.
From the given equation
x – 2y = 6 …(i)
Expressing x in terms of y, we get
x = 2y + 6
when y = 0, x = 2 × 0 + 6 = 6

Now plotting and joining the points (RBSESolutions.com) from table (i) and (ii) on the same graph paper, we find that their is no point of intersection i.e. no solution i.e. lines goes parallel to each other.

Question 4.
x + y = 4; 2x – 3y = 3
Solution.
From the given equation
x + y = 4
⇒ y = 4 – x …(i)
when x = 0, y = 4 – 0 = 4


Now plotting and joining the (RBSESolutions.com) points from table (i) and (ii) on the same graph paper,
we find that their point of intersection is (3, 1).
Hence, (3, 1) is the required solutions.

Question 5.
2x – 3y + 13 = 0; 3x – 2y + 12 = 0
Solution.
From the given equation
2x – 3y + 13 = 0



Now plotting and joining the points (RBSESolutions.com) from table (i) and (ii) on the same graph, we find that their point of intersection is (- 2, 3).
Hence, the required solution is (- 2, 3).

Question 6.
3x – 4y = 1; \(-2x+\frac { 8 }{ 3 }y=5\)
Solution.
From the given equation
3x – 4y = 1
=> 4y = 3x – 1



Now plotting and joining the points from (RBSESolutions.com) table (i) and (ii) on the same graph paper we find that these lines are parallel to each other it means no solution.
Hence, the system of equations has no solutions.

Question 7.
\(2x+\frac { y }{ 2 }-5=0\); \(\frac { x }{ 2 }+y=-4\)
Solution.
From the given equation
\(2x+\frac { y }{ 2 }-5=0\)
4x + y – 10 = 0
⇒ y = – 4x + 10
⇒ y = 10 – 4x …..(i)


Plot all above points (- 2, – 3), (- 4, – 2), (- 6, – 1) and (4, – 6) on the same (RBSESolutions.com) graph paper and join them and get the graph CD (Line segment).
The point of intersection of AB and CD is P(4, – 6) therefore the required solution is x = 4 and y = – 6.

Question 8.
0.3x + 0.4y = 3.2; 0.6x + 0.8y = 2.4
Solution.
The above equations can also be written as
3x + 4y = 32 …(i)
and 6x + 8y = 24 …(ii)


Now plotting and joining the points from (RBSESolutions.com) table (i) and (ii) on the same graph paper. We find that the lines goes parallel to each other. Hence the system of equation has no solution.

Question 9.
2x + 3y = 8; \(4x-\frac { 3 }{ 2 }y=1\)
Solution.
We have,
2x + 3y = 8
\(4x-\frac { 3 }{ 2 }y=1\)



Plot the above pair of points from table (i) and table (ii) on the (RBSESolutions.com) same graph paper. Join them. After joining we find that the point of intersection of both the lines is (1, 2).
Hence, x = 1, y = 2 is the required solution.

Question 10.
3x – y = 2; 6x – 2y = 4
Solution.
Consider the equation 3x – y = 2
Expressing y in terms of x, we get
y = 3x – 2 …(i)
when x = 0, y = 3×0 – 2 = -2
when x = 1, y = 3×1 – 2 = 1
when x = 2, y = 3×2 – 2 = 4


Now plotting and joining the points from table (i) and (ii) we (RBSESolutions.com) find that the lines overlapping each other i.e. all the points coincide with each other. It means the system of equations has infinitely many solutions.

Question 11.
3x + 2y = 0; 2x + y = -1
Solution.
From the given equation
3x + 2y = 0
We 2y = -3x


Now plot the points (1, – 3), (- 1, 1) and (- 2, 3) on the same (RBSESolutions.com) graph paper, join these points and obtain the line CD i.e. the graph of the equation 2x + y = – 1.
From the graph of two equations we see that AB and CD intersect and the coordinates of the point of intersection is (-2, 3)

Hence, x = – 2, and y = 3 is the required solution.

We hope the given RBSE Solutions for Class 9 Maths Chapter 4 Linear Equations Ex 4.1 in Two Variables will help you. If you have any query regarding Rajasthan Board RBSE Class 9 Maths Solutions Chapter 4 Linear Equations in Two Variables Ex 4.1, drop a comment below and we will get back to you at the earliest.