RBSE Solutions for Class 10 Maths Chapter 4 Linear Equation and Inequalities in Two Variables Ex 4.2

RBSE Solutions for Class 10 Maths Chapter 4 Linear Equation and Inequalities in Two Variables Ex 4.2 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 4 Linear Equation and Inequalities in Two Variables Exercise 4.2.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 10
Subject	Maths
Chapter	Chapter 4
Chapter Name	Linear Equation and Inequalities in Two Variables
Exercise	Ex 4.2
Number of Questions Solved	2
Category	RBSE Solutions

Rajasthan Board RBSE Class 10 Maths Chapter 4 Linear Equation and Inequalities in Two Variables Ex 4.2

Question 1
By graphical method, show the (RBSESolutions.com) solution set of the following inequalities :
(i) x ≥ 2
(ii) y ≤ -3
(iii) x – 2y < 0
(iv) 2x + 3y ≤ 6
Solution:
(i) Given inequality x ≥ 2
writing its equation form, x = 2
It is clear that straight line is parallaled to y-axis and will pass through point (2, 0) of x-axis and
obtained the following graph.

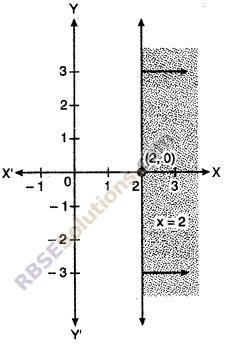
Graph of two meeting (RBSESolutions.com) points is as follows:

Now, inequality 2x + 3y ≤ 6 satisfied by origin (0, 0). Therefore region from line to origin, shaded part is required solution set.

Question 2
Solve the following (RBSESolutions.com) inequalities, graphically:
(i) \(\left| x \right| \le 3\)
(ii) 3x – 2y ≤ r + y – 8
(iii) \(\left| x-y \right| \ge 1\)
Solution:
(i) Removing modules from given \(\left| x \right| \le 3\)
inequality \(\left| x \right| \le 3\), we get
⇒ -3 ≤ x ≤ 3
⇒ x ≤ 3 ……(i)
and x ≥ -3 ………..(ii)
writing inequality (j) in equation form,
x = 3
line x = 3, will be right side of y – axis and
parallel to y-axis writing (RBSESolutions.com) inequality (ii) in equation form, r = -3.
Line x = -3, will be left side of y-axis and ॥ to y-axis.
Graph of both linear equations is as follows:

Thus, inequality \(\left| x \right| \le 3\) satisfy by origin (0,0)
Therefore, shaded part from line x = 3 to
x = -3 will be (RBSESolutions.com) required solution set.

(ii) Given inequality 3x – 2y ≤ x +y – 8 writing this, in equation form, we get
3x – 2y = x + y – 8
⇒ 3x – x – 2y – y = -8
⇒ 2x – 3y = -8
Putting x = 0 in equation, we get
2 x o – 3y = -8
-3y = -8
y = \(\frac { 8 }{ 3 }\)
point ( 0, \(\frac { 8 }{ 3 }\)) will cut y – axis.
Now, putting y = 0,
2x – 3 x 0 = -8
x = -4
Point (-4, 0) will cut x – axis.
Graph obtained from (RBSESolutions.com) two points will be as follows:

Thus, inequality 3x – 2y ≤ x + y – 8 does not satisfied by origin (0, 0).
⇒ 3 x 0 – 2 x 0 ≤ 0 + 0 – 8 which is not true.
Therefore shaded area opposite to origin from line will be required solution set.

(iii) Given (RBSESolutions.com) inequality
\(\left| x-y \right| \ge 1\)
Removing modulus, we get
x – y ≥ 1
and x – y ≤ -1
writing in equation form, we get
x – y = 1 ……(i)
or x – y = -1 …(ii)
In equation (i),
Putting x = 0, 0 – y = 1
y = -1
Point (0,-1) will lie on y – axis.
Now, putting y = 0,
x – 0 = 1
x = 1
Point (1, 0) will lie on x – axis.
from equation (ii),
Putting x = 0, 0 – y = -1
y = 1
Point (0, 1) will lie on y – axis.
Now, putting y = 0
x – 0 = -1
x = -1
Point (-1, 0), will lie on x – axis.
By joining (RBSESolutions.com) points (0,-1), (1, 0) and (0, 1), (-1, 0), following graph is obtained:

Now, inequality x – y ≥ 1 does not satisfied by origin (0, 0).
Its shaded (RBSESolutions.com) portion will be the region from line to opposite to origin.
Second inequality x – y ≤ -1 also not satisfied by origin (0,0)
i.e., 0 – 0 < -1 is not true.
Therefore its shaded part will be the region from line to opposite to origin.

We hope the given RBSE Solutions for Class 10 Maths Chapter 4 Linear Equation and Inequalities in Two Variables Ex 4.2 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 4 Linear Equation and Inequalities in Two Variables Exercise 4.2, drop a comment below and we will get back to you at the earliest.